MATEMÁTICA

Seja bem vindo!

PORTFÓLIO

MATEMÁTICA

Polo: Araçatuba – São Paulo

Mediadora – Denise Gregory Trentin

Curso: Licenciatura em Ciências Naturais e Matemática

Discente: Gracielli Mendes Abuchaim

Docente: Nilson José Machado

Matéria: Matemática

Semana:1

Vídeo:1

Tema: Lógica, Matemática e linguagem cotidiana (I)

https://www.youtube.com/watch?v=__m60SKn-Dw

A matemática refere-se a uma linguagem relacionada com a língua materna. Sua linguagem é inesgotável por possuir um conjunto de técnicas que fazem os cálculos além de conteúdos com idéias fundamentais que formam a sua caracterização. Segundo o senso comum a matemática é fundamental para desenvolver o raciocínio, mas para fonte primária do raciocínio é necessário a presença da língua, pois existe uma relação de dependência com o cotidiano por ter uma característica marcante com sentenças declarativas que contém o sendo verdadeiro ou falso.  A linguagem matemática necessita da precisão e limitação para as suas sentenças poderem ser precisam e classificadas. Para se conseguir esses recursos precisamos retirar as sentenças históricas. Segundo Aristóteles, todos os ensinamentos determinam que devemos ser mais diretos sendo em afirmações ou negações que envolve coisas desconhecidas, onde a pessoa que faz a leitura precisa interpretar o questionamento como forma de pergunta. Devemos ter me mente que as equações são perguntas, onde o problema nasce de uma pergunta com linguagem corrente precisando das idéias matemáticas para solucionar as situações.

Devemos seguir as regras apresentadas para podermos compreender as definições da matemática.
Fonte: www.portfoliounivespplucianegallo.blogspot.com
Vídeo:2

Docente:Nilson José Machado

Tema: Lógica, Matemática e linguagem cotidiana (II)

https://www.youtube.com/watch?v=HkYslTNbp8o

Ao falarmos em lógica devemos lembrar que ela trata de argumentos que defendem a verdade de uma sentença com razões que confirmam para mim o porquê de a sentença ser verdadeira. Sempre existe a premissa e a conclusão. Quando demonstramos se uma preposição é verdadeira construímos a validade dela. Ocorre a argumentação com a defesa onde a lógica não entra no conteúdo das preposições entrando apenas nas verdades faladas. A lógica formal cuida da forma da argumentação. A defesa da verdade de uma conclusão depende da versão e da verdade das premissas.

Se entendermos que as sentenças e proposições estão a nossa disposição para compreendermos a relação entre o que é verdadeiro e falso facilitará o entendimento desse conteúdo.
Fonte: www.slideplayer.com.br
   Vídeo:3

Docente: José Luiz Pastore Mello

Tema: Números: uma visão histórica; os números √2 ,π, φ (I)

https://www.youtube.com/watch?v=JggRQXlksmY

Os números recebem uma classificação, entre eles existem os números naturais utilizados para contagem, sendo que entre eles existem a presença dos números negativos que foi introduzido a partir do período de comércio. Devemos saber que nem todos os números racionais são inteiros. O numero é racional quando pode ser escrito em forma de fração com presença de numerador inteiro segundo a fala do professor. Nesse contexto existem também os números racionais que incorporam os irracionais que não são escritos de forma inteira e por este motivo não podem ser escritos na forma de fração. Entre os conjuntos naturais existem os subconjuntos sendo eles os primos, entre os números inteiros existem os que não são naturais. Um matemático chamado Euclides respondeu a questão da quantidade de números primos chegando a conclusão que os números primos são infinitos, isso tudo através de uma hipótese com uma contradição, pois a distribuição de números primos é muito complexa por ter infinitos elementos. Contudo a relação entre a matemática com os números é bastante diversificada e deve ser analisada atentamente.

A representação das figuras explicam as diferenças entre os números naturais e irracionais.
Fonte: www.slideplayer.com.br
Vídeo:4

Docente: José Luiz Pastore Mello

Tema: Números: uma visão histórica; os números √2, π, φ (II)

https://www.youtube.com/watch?v=ACdH47ECOcY

Raiz quadrada (√) e fi (φ) são também números irracionais, que devem ser analisados segundo a aula apresentada. O professor utilizou um exemplo feito coma folha de papel sendo ela a sulfite mais usada por nós sendo ela uma folha com representação A4 que tem a proporção de 210 mm X 297 mm ,e razão áurea 1,618. Isso tudo ocorre devido a existência de um padrão. Um outro exemplo citado foi em relação aos retângulos que nem sempre são semelhantes pois para que ocorra, a razão do menor tamanho tem que ser igual a do maior tamanho (isso quando falamos em lados). Já em relação a razão áurea que também pertence a um número irracional com infinitas casas e com inúmeras utilizações aproximadas, o estudioso Leonardo Fibonacci demonstra a proporção e define que os problemas matemáticos devem ser considerados como um desafio a ser resolvido.

As figuras representam os números irracionais e também a representação Áurea.

Fonte: www.curiosidadenamatematica.blogspot.com

           www.beatrizotto.blogspot.com

Exercícios da semana 1 – video aulas 1 e 2

RECOMENDAÇÕES GERAIS SOBRE A AVALIAÇÃO (PORTFÓLIO)

Caro aluno,

Nesta semana, a sua avaliação para as aulas 1 e 2 será composta por duas entregas no Portfólio de Matemática que estão descritas a seguir:

A)   Para avaliação das aulas 1 e 2 da Semana 1 da disciplina, escreva um resumo pessoal, de 10 a 20 linhas, sobre o significado do tema tratado, registrando em que as aulas contribuíram para revelar o papel da Matemática na compreensão da realidade. Publique sua resposta no Portfólio da disciplina.

Revelar o papel da Matemática na compreensão da realidade.

Lógica, Matemática e linguagem cotidiana

Compreendi através da explicação do professor que a matemática é fundamental para a relação humana, pois é através dela que conseguimos compreender e desenvolver técnicas eficientes para resolução de problemas. Na relação com os cálculos precisamos estabelecer alguns recursos  dinâmicos que facilitam a compreensão e a análise das representações onde podemos argumentam nossas idéias utilizando os recursos adequados e também com clareza. Afinal, segundo o professor, a linguagem matemática é transformada em uma afirmação que envolve coisas desconhecidas, permitindo as pessoas que façam uma leitura precisa com interpretação dos questionamentos como forma de pergunta. Portanto, devemos ter em mente que as equações são perguntas, onde o problema nasce de uma pergunta com linguagem corrente precisando das idéias matemáticas para solucionar as situações.

B)   Os exercícios das aulas 1 e 2, foram formuladas a partir de pequenos textos (Texto A, Texto B, Texto C etc.). Para avaliação das aulas 1 e 2, escolha pelo menos UM (1) Texto (A, B, C etc.)  e resolva os exercícios relacionados ao texto. As respostas devem ser  enviadas pelo Portfólio da disciplina.  Para melhorar a sua aprendizagem resolva, explore e aprofunde, até onde for possível, os outros textos e seus exercícios.

Conforme a explicação acima, resolverei para análise o TEXTO (B).

Lembre-se - você também deverá entregar alguns exercícios referentes às video aulas 3 e 4 que podem ser acessados na Organização Didática da semana 1 disponível no Ambiente Virtual de Aprendizagem (AVA) do curso.

Exercícios das vídeoaulas 1 e 2 – Matemática

TEXTO B

Uma proposição (sentença verdadeira ou falsa) isolada não caracteriza um argumento. Nem uma simples coleção de proposições é um argumento. Argumentar é justificar a verdade de uma proposição (que é a conclusão do argumento) como consequência lógica da verdade outras proposições (que são as premissas do argumento). A estrutura geral de um argumento é “se p é verdade, então q também será”, em que p representa uma ou mais proposições. Um argumento sempre apresenta uma proposição que é a conclusão, e uma ou mais premissas que a justificam.

5.    Em cada texto abaixo, indique se se trata ou não de um argumento:

a)    Acho que vai chover. (F) Não é um argumento

b)    Amanhã deverá fazer sol, porque o serviço de meteorologia previu muita chuva, e ele tem errado em suas previsões. (V) É um argumento

c)    Joaquim é português e é dono da maior padaria do bairro, que produz 10 000 pães por dia. (V) É um argumento

d)    Joaquim não é português, pois ele nasceu no Brasil, e quem nasce no Brasil é brasileiro. (V) É um argumento

e)    Penso muito na vida. (F) Não é um argumento

f)     Penso, logo, existo. (V) É um argumento

6.    Em cada argumento abaixo, indique qual é a conclusão e quais são as premissas:

a)    “É lógico que o time C é o melhor do atual campeonato, pois ele tem o melhor ataque, a defesa menos vazada e o maior número de vitórias.” Conclui-se que esse time é mais desenvolvido pois segundo a argumentação é capaz em todas as habilidades além de apresentar premissas que capacitam suas habilidades pois representam todas as características do time citado.

b)    “Três séculos de pesquisas mostraram-nos que nenhum megalozoário é carcomênico. Deste fato, podemos concluir que os infimozoários não são carcomênicos, uma vez que todo infimozoário é megalozoário”. A relação entre os megalozoários, os carcomênicos e os infilozoários está sendo representada de maneira errada, pois a lógica entre eles não representa que ambos estão relacionados juntamente. Conclui-se que os megalozoários são também carcomênicos e que os infilozoários não são megalozoários.

c)    “O café não é um produto importado; portanto, não deveria ser caro, uma vez que todos os produtos importados é que são caros. Para que possamos estabelecer um raciocínio sobre o que é caro e o que é barato é necessário haver uma premissa mais esclarecedora, pois da maneira como está sendo dita não há possibilidade de afirmar se são realmente caros todos os produtos importados.

Exercícios da semana 1 – vídeo aulas 3 e 4

RECOMENDAÇÕES GERAIS SOBRE A AVALIAÇÃO (PORTFÓLIO)

Caro aluno,

Nesta semana, a sua avaliação para as Aulas 3 e 4 será composta por duas entregas no Portfólio de Matemática que estão descritas a seguir:

A) Os exercícios da aula 3 foram formulados para que pratique aquilo que aprendeu na video aula. Para avaliação da aula 3, escolha pelo menos UM (1) exercício  para resolver. A resposta deve compor o Portfólio da disciplina.  Para melhorar a sua aprendizagem resolva, explore e aprofunde, até onde for possível, os outros exercícios da aula 3.

B) Os exercícios da aula 4, foram formulados para que pratique aquilo que aprendeu na video aula. Para avaliação da aula 4, escolha pelo menos UM (1) exercício  para resolver. A resposta deve compor o Portfólio da disciplina.  Para melhorar a sua aprendizagem resolva, explore e aprofunde, até onde for possível, os outros exercícios da aula 4.

 Lembre-se - Nesta semana você também deverá postar a resolução de alguns exercícios referentes às videoaulas 1 e 2 que estão disponíveis na Organização Didática da semana 1 e no Ambiente Virtual de Aprendizagem (AVA) do curso.

 Exercícios da video aula 3

Números: uma visão histórica (I)

Prof. José Luiz Pastore Mello

 Conforme a solicitação realizei a atividade do exercício nº 5

5)    Na vídeo aula que você assistiu, sugere-se o seguinte resultado sobre números racionais e sua representação decimal:

Um número racional p/q tem ou representação decimal finita, ou representação decimal infinita e periódica. Se p/q é uma fração irredutível, então esse número terá representação decimal infinita e periódica apenas se na fatoração em números primos de q encontrarmos algum fator primo diferente de 2 e de 5.

Dê exemplos de frações irredutíveis p/q cuja representação decimal seja finita, e exemplos de frações irredutíveis p/q cuja representação decimal seja infinita e periódica. No segundo caso, explicite o fator primo da fatoração de q que faz com que p/q seja uma dízima periódica.

R: As frações decimais e as que lhes são equivalentes são sempre representadas por dízimas finitas.

As frações que não são decimais ou equivalentes são sempre representadas por dízimas infinitas periódicas.

Verificamos que:

Neste caso, é apenas o algarismo 6 que se repete infinitamente.

Desta vez, verificamos que:

Neste caso, repete-se infinitamente a sequência 45.

Exercícios da video aula 4

Números: uma visão histórica (II)

Conforme a solicitação realizei a atividade do exercício nº 1

1)    Na vídeo aula você viu que todos os papeis da chamada “série A” são retângulos que, quando dobrados ao meio pelo eixo de simetria perpendicular ao maior lado, geram retângulos semelhantes ao retângulo original. Dizendo de outra forma, são retângulos cuja razão entre o maior e o menor lado é igual ao número irracional .

A maior folha retangular da série A de papel, denominada folha A0, além de atender à condição que define a série, possui 1 m² de área. Determine o comprimento e a largura do papel A0.

R: O formato da série A é baseado em uma folha de papel de 1 m2, com dimensões

841 mm 1189 mm.

Designação       Dimensão

         A0              841X1189

Formato: Margem esquerda = 25 e Margem direita = 10

                  Largura da linha do quadrado = 1,4

Semana:2

Vídeo:5

Docente: Roberto Perides Moisés

Tema: Geometria: medidas, áreas e volumes (I)

https://www.youtube.com/watch?v=7B0KoMKmH8U

A Geometria deve ser entendida através de uma pesquisa histórica desde seu o surgimento no Egito com referências as pirâmides, o deserto e o rio Nilo, pois o homem através desses conceitos precisou compreender e lidar com as medidas planadas na terra. Já sobre as pirâmides podemos pensar que as figuras mais simples existentes são os prismas (serrar). Ex: baralho que tem figura plana e que permite a sobreposição de figuras e com isso podemos formar um prisma. Contudo, a figura espacial é formada a partir do empilhamento das figuras planas. Segundo o matemático Cavaliere as figuras planas são compostas por linhas empilhadas e isso forma os empilhamentos das figuras planas (o volume é formado pela área multiplicada pela altura). A altura é a distância entre as bases. A área da base pode ser a mesma quando comparamos os prismas oblíquos com os retos. A geometria da forma em movimento refere-se à construção de figuras sólidas com o empilhamento das figuras planas. Todas as faces laterais de um prisma são retangulares e os triângulos devem ter todos os ângulos iguais.

A transformação ocorre a partir da construção do novo e isso é possível devido ao saber introdutório sobre a geometria que ilustra todas as figuras acima.
Fonte: www.leonidantas.blogspot.com
          www.manualescolar.2.0.sebenta.pt
Vídeo:6

Docente: Roberto Perides Moisés

Tema: Geometria: medidas, áreas e volumes (II)

https://www.youtube.com/watch?v=eL0WEIIxZYE

As pirâmides nos remetem as pirâmides do Egito onde pensamos nas figuras com o pensamento em sua forma plana passando por um processo de decomposição planificada. Na pirâmide encontramos o vértice com conversão de laterais, arestas laterais, arestas da base e altura com projeção ortogonal onde o vértice sobre a base acaba caindo no centro do polígono. Quando a base da pirâmide for um polígono regular com pirâmide reta a figura se torna uma pirâmide também regular. Verificando as figuras apresentadas podemos visualizar as diminuições das figuras formando o afunilamento das pirâmides. Existe na pirâmide um elemento presente em todos os polígonos regulares ( inscrevem uma circunferência). A distância entre o centro da figura tem o apótema onde colocamos a ponta do compasso, e por a pirâmide ser um corpo que afunila sua medida deve ter volumes com base e altura de prisma menor.

As figuras representam a geometria através de suas imagens que permitem a relação entre a medida, área e volume.
Fonte: www.matematiques.com.br
           www.mundoeducacao.com

Vídeo:7

Docente: Nilson José Machado

Tema: Álgebra - uma introdução (I)

https://www.youtube.com/watch?v=4Sp5kunaXGE

A álgebra possui um nível inicial que deve ser articulado entre as grandezas que são associadas a ela. Já no segundo nível verificamos as propriedades dos números, após devemos conceituar as generalizações onde as letras se tornam corporativas e por fim, esses processos entram na elaboração das equações com a percepção de um olhar diferenciado sobre o conjunto numérico afinal, a álgebra inicia-se com o nosso conhecimento dos níveis que ela representa.

É através da álgebra que conseguimos desenvolver melhor nosso raciocínio.
Fonte: www.mat.ufmg.br
           www.render.com.br
Vídeo:8

Docente: Nilson José Machado

Tema: Álgebra - uma introdução (II)

https://www.youtube.com/watch?v=M_Iyyx0h4SM

Quando iniciamos os números vemos que eles se associam as grandezas e isso permite a resolução das perguntas matemáticas por desenvolvimento de técnicas. Uma equação por ser a tradução de uma pergunta pode ser variada com questionamentos complexos, pois, nesse contexto utilizamos as letras e os números sendo que as propriedades são utilizadas para recuperação do valor do x nas equações. Sabe-se que as equações diferem em primeiro, segundo, terceiro entre outras e sobre a álgebra nesse quesito é preciso que se faça a fatoração (descobrir dois fatores que multiplicados resumem a expressão) para transformar a equação. Fatoração é o recurso de excelência para podermos resolver as frações. Toda equação de grau n tem sempre n raízes segundo a fala do professor e a forma mais adequada de resolver é o seguimento das equações para podermos utilizar a tecnologia da álgebra e buscar os resultados. As relações entre os elementos possuem conjuntos estruturados com representações características.

A álgebra permitiu a transformação dos cálculos matemáticos.
Fonte: www.clasf.com.br
          www.twitter.com

Exercícios da semana 2 / vídeo aulas 5 e 6

EXERCÍCIO 1

Faça uma pesquisa sobre o Teorema de Pitágoras. Escreva seu enunciado, apresente e discuta uma demonstração e, ao final, crie um exercício acompanhado de sua resolução.

O Teorema de Pitágoras é considerado uma das principais descobertas da Matemática, ele descreve uma relação existente no triângulo retângulo. Vale lembrar que o triângulo retângulo pode ser identificado pela existência de um ângulo reto, isto é, medindo 90º. O triângulo retângulo é formado por dois catetos e a hipotenusa, que constitui o maior segmento do triângulo e é localizada oposta ao ângulo reto. Observe:

Catetos: a e b
Hipotenusa: c

O Teorema diz que: “a soma dos quadrados dos catetos é igual ao quadrado da hipotenusa.”

a² + b² = c²

Exemplo 1
Calcule o valor do segmento desconhecido no triângulo retângulo a seguir.

x² = 9² + 12²
x² = 81 + 144
x² = 225
√x² = √225
x = 15
Foi através do Teorema de Pitágoras que os conceitos e as definições de números irracionais começaram a ser introduzidos na Matemática. O primeiro irracional a surgir foi √2, que apareceu ao ser calculada a hipotenusa de um triângulo retângulo com catetos medindo 1. Veja:

x² = 1² + 1²
x² = 1 + 1
x² = 2
√x² = √2
x = √2
√2 = 1,414213562373....

EXERCÍCIO 3

Rotacionando um quadrado de lado 2 cm em torno de um eixo que passa por um de seus lados obtemos um cilindro circular reto, como mostra a figura. Determine a área total do cilindro e seu volume.

b) área da base ( A_B):área do círculo de raio r

c) área total ( A_T): soma da área lateral com as áreas das bases

Vcilindro = ABh

           No caso do cilindro circular reto, a área da base é a área do círculo de raio r ;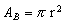

portanto seu volume é:

Solução. Observando a figura formada na base do cilindro, vemos um círculo inscrito no quadrado de lado 2cm. O raio do círculo vale a metade do lado, isto é, r = 1cm.  A altura do cilindro coincide com a aresta vertical do cubo. Logo temos os cálculos:

i) Área da base: p(1)² = pcm²

ii) Volume: (p)(2) = 2pcm³ = 2.(3,14)cm³ = 6,28cm³.

Exercícios da semana 2 / vídeo aulas 7 e 8

Álgebra – Uma introdução

Números e letras de mão dadas

Caro aluno,

Nesta semana, a sua avaliação para as Aulas 7 e 8 será composta por

duas entregas no Portfólio de Matemática que estão descritas a seguir: 

Para avaliação das aulas 7 e 8, escolha pelo menos dois (2) exercícios para resolver.

 EXERCÍCIOS

Texto 2

1-    Procure um livro em que a dedução da fórmula de Bhaskara seja realizada e acompanhe passo a passo para entender como ela surge.

Fórmula de Bhaskara foi dada em homenagem ao matemático Bhaskara Akaria, considerado o mais importante matemático indiano do século XII.

A fórmula de Bhaskara é principalmente usada para resolver equações quadráticas de fórmula geral ax²+bx+c=0, com coeficientes reais, com a≠0 e é dada por:

 chamamos de discriminante: Δ = b²-4ac

Dependendo do sinal de Δ, temos:

• Δ=0, então a equação tem duas raízes iguais.
• Δ>0, então a equação tem duas raízes diferentes.
• Δ<0, então a equação não tem raízes reais.

A ideia da demonstração da fórmula de Bhaskara é o completamento de quadrados. Seja:

ax²+bx+c=0
a²x²+abx+ac=0
4a²x²+4abx+4ac=0
4a²x²+4abx+b²+4ac=b²
(2ax)²+2(2ax)b+b²=b²-4ac
(2ax+b)²=b²-4ac

Através da Fórmula de Bhaskara podemos deduzir uma expressão para a soma (S) e o produto (P) das raízes da equação do 2º grau.

Sendo x₁ e x₂ raízes da equação ax²+bx+c=0, então:

S = x₁+x₂ = -b/a

P = x_1.x₂ = c/a

A importância da Fórmula  de Bhaskara é que ela nos permite resolver qualquer problema que envolva equações quadráticas, os quais aparecem em diversas situações importantes, como na Fisica por exemplo.

TEXTO 5 

Busque em um livro de Álgebra as definições das estruturas algébricas

mais simples: semi-grupo, grupo, anel e corpo

Semi-grupo pode ser definido de 2 maneiras completamente equivalentes

1.   é um conjunto G dotado de uma operação binária para a qual valem as seguintes propriedades:

1.  fechamento: dado a,b∈G o elemento resultante da composição de a e b pertence a G (a∗b∈G)

2.  associatividade: para todos a,b,c∈G vale (a∗b)∗c=a∗(b∗c)=a∗b∗c

2.   é um grupóide dotado da propriedade associativa (associatividade)

1.  associatividade: para todos a,b,c∈G vale (a∗b)∗c=a∗(b∗c)=a∗b∗c

Grupo é um conjunto de elementos associados a uma operação que combina dois elementos quaisquer para formar um terceiro. Para se qualificar como grupo o conjunto e a operação devem satisfazer algumas condições chamadas axiomas de grupo: associatividade, elemento neutro e elementos inversos. Apesar destes serem comuns a muitas estruturas matemáticas familiares - e.g. os números inteiros munidos da adição formam um grupo - a formulação dos axiomas é independente da natureza concreta do grupo e sua operação. Isso permite lidar-se com entidade de origens matemáticas completamente diferentes de uma maneira flexível, mas retendo os aspectos estruturais essenciais de muitos objetos da álgebra abstrata e além. A ubiquidade dos grupos em inúmeras áreas - dentro e fora da matemática - os tornam um princípio organizador central da matemática contemporânea.

 Anel é uma estrutura algébrica que consiste num conjunto A  com um elemento 0 e duas operações binárias + e  que satisfazem as seguintes condições:

1.   Associatividade de  + :

2.   Existência de elemento neutro (0) de +: 

3.   Existência de simétrico de + :

4.   Comutatividade de  + :

5.   Associatividade de  x : 

6.   Distributividade de  em relação a +  (à esquerda e à direita): 

Corpo

Mais formalmente, um anel comutativo F com unidade é chamado de corpo se:

Resulta da comutatividade de F  que o y da definição anterior também satisfaz a condição y.x= 1. Por outro lado, só pode haver um único y naquelas condições. De fato, se y  e  forem tais que  então 

Este elemento y designa-se por inverso de x e representa-se por 

Um corpo F  não tem divisores de zero. Efectivamente, se x e y forem dois elementos de F diferentes de 0 então X.Y ≠ 0 pois ≠ 0.

Mas se se tivesse x.y= 0, então ter-se-ia .

Semana:3

Vídeo:9

Docente: Walter Spinelli

Tema: Representações, Gráficos, Transformações (I)

https://www.youtube.com/watch?v=K_bEDo47tj0

No estudo das funções as transformações que modificam a estrutura do gráfico permitem que eles transformem o plano cartesiano. Nesse sentido a função a e b torna-se  x que corresponde ao y. Quando nos referimos ao x precisamos saber que seus valores devem ser esgotados. A sentença matemática é representada como F-X.  Nas abscissas todos os valores de x serão trocados e passarão a ser negativos. Em relação ao eixo das ordenadas ocorre a alteração dos valores de x. Toda composição de uma função, permite a ocorrência das alterações.

As transformações são possíveis devido as representações existentes entre os ângulos.
Fonte: www.scilo.org.mx

 Vídeo:10

Docente: Walter Spinelli

Tema: Representações, Gráficos, Transformações (II)

https://www.youtube.com/watch?v=7AIVCaOrTmY

A função linear remete a função do y= a x+b e essa equação faz com que o A tenha relação com a inclinação do eixo x e o B refere-se ao corte (reta gerada). A multiplicação dos valores faz com que o gráfico gere outro gráfico sendo ele simétrico em relação ao já existente. Quando a função é negativa as retas são modificadas. As reflexões causadas pelo negativo da função não são evidentes. O coeficiente A da parábola tem relação direta fazendo que a equação tenha uma curva fechada.  Quando o coeficiente é negativo a concavidade se volta para baixo. A constante permite que o gráfico faça translações horizontais, mas quando acrescentamos elementos na função ela se desloca e modifica a estrutura se deslocando verticalmente. Na reflexão em relação a reta bissetriz dos quadrantes o contexto das coordenadas de um ponto precisa ser invertido.

Entre as representações dos ângulo em x e y a figura linear consegue representar a inclinação.

Fonte: www.ime.unicamp.br

Vídeo:11

Docente: José Luiz Pastore Mello

Tema: Sequências (I)

https://www.youtube.com/watch?v=1T79kdwwBEY

Seqüências numéricas são expressadas através de conceitos elaborados com valores, sendo eles uma função que associa aos números naturais um valor real, fazendo com que a razão de um termo seja constante ao segundo termo. A fórmula de recorrência define um primeiro valor com todos os termos seguintes calculares em termos anteriores. Existem fórmulas que não são recorrentes por não depender de conhecimento do termo. Já as seqüências aritméticas posicionais sempre serão uma função de primeiro grau sendo sua fórmula y= a x+b. A fórmula de recorrência n=1 gera um ponto; n= 2 gera dois pontos e assim ocorre a continuidade dos fatores. Em relação a fórmula posicional, ela permite a mudança da posição dos quadrados posicionados. Já a fórmula de recorrência está sempre dependendo de um primeiro termo.

As sequências matemática podem ser representadas de várias formas, sendo uma dela a presente na figura a cima.
Fonte: www.infinito-matematica.co

Vídeo:12

Docente: José Luiz Pastore Mello

Tema: Sequências (II)

https://www.youtube.com/watch?v=V2CBly9ELow

As seqüências podem ser desenvolvidas de várias maneiras, sendo as mais analisadas a aritmética e geométrica. Após conhecer a seqüência de Grandi pude compreender que sua referência a números alternados facilita a análise dos cálculos. Quando a aula apresentou as séries e suas definições dizendo que sua seqüência ocorre com números infinitos e que sua soma define a sua ação tornou possível a compreensão das funções de uma série.

O seguimento representativo é muito significativo nas relações entre a imagem desta figura.

Fonte: www.pessoal.sercomtel.com.br

Exercícios  /  aulas 9 e 10

RECOMENDAÇÕES GERAIS SOBRE A AVALIAÇÃO (PORTFÓLIO)

Caro aluno,

Nesta semana a sua avaliação para as aulas 09 e 10 será composta

por duas postagens no Portfólio de Matemática que estão descritas a

seguir:

A. Os exercícios da aula 9 foram formulados para que pratique aquilo

que aprendeu na vídeoaula. Para avaliação da aula 9, escolha pelo

menos UM (1) exercício para resolver.

A generalização da representação de números por letras é o entendimento direto da álgebra. A linguagem cotidiana envolve várias sentenças, mas a linguagem matemática deve envolver sentenças declarativas sem presença de perguntas. As equações devem ser entendidas como resolução das perguntas que demonstram situações problemas que precisam de uma equação para solucioná-los. As pirâmides tem área equivalente se tiver mesma base e mesma altura. Portanto, a partir de prisma triangular com volumes de base igual e mesma altura encontrar o volume equivalente para as pirâmides. O cone é feito de um círculo com figura plana, com junção de extremidades que transforma a figura em espacial gerando o vértice do cone.

 B. Os exercícios da aula 10, foram formulados para que pratique aquilo que aprendeu na vídeoaula. Para avaliação da aula 10, escolha pelo menos UM (1) exercício para resolver.

Gráfico da função f(x) = x²

 

1.  Desenhe num mesmo plano cartesiano as parábolas que representam as funções f(x) = x2 e g(x) = (x – 3)2 – 3. Compare os dois gráficos e descreva as transformações que podemos impor ao gráfico de f(x) para que ele coincida com o gráfico de g(x).

Exercícios / aulas 11 e 12

RECOMENDAÇÕES GERAIS SOBRE A AVALIAÇÃO (PORTFÓLIO)

Caro aluno,

Nesta semana, a sua avaliação para as aulas 11 e 12 será composta por duas entregas no Portfólio de Matemática que estão descritas a seguir 
A. Os exercícios da aula 11, foram formulados para que pratique aquilo que aprendeu na vídeo aula. Para avaliação da aula 11, escolha pelo menos UM (1) exercício para resolver. A resposta deve ser  enviada pelo Portfólio da disciplina.

B. Os exercícios da aula 12, foram formulados para que pratique aquilo que aprendeu na vídeo aula. Para avaliação da aula 12, escolha pelo menos UM (1) exercício para resolver. A resposta deve ser  enviada pelo Portfólio da disciplina.

A)     n = 1 n = 2 n = 3 n = 4

a) Posicional: an = n²

A1 = 1
A2 = 2² = 4
A3 = 3² = 9
A4 = 4² = 16

Recursiva : an = a(n-1) + (n -1) + n
A1 = 1
A2 = 1 + (2 – 1) + 2 = 4
A3 = 4 + (3 – 1) + 3 = 9
A4 = 9 + ( 4 – 1) + 4 = 16

 A soma dos infinitos termos de uma progressão geométrica de primeiro termo a1 e razão q entre -1 e 1 é dada pela fórmula   . Usando essa informação, determine a fração geratriz das dízimas periódicas indicadas abaixo:
a) 0,7777…. b) 0,161616… c) 0,23333…

a) 0,7 + 0,07 + 0,007

 a1 = 0,7; q = 0,1

S=  {0,7} over {1-0,1} =  {0,7} over {0,9} =  {7} over {9}

 b) 0,16 + 0,0016 + 0,000016

a1 = 0,16; q = 1/100

S=  {0,16} over {1-0,01} =  {16} over {99}

 c) 0,2 + 0,03 + 0,003

a1 = 0,03; q = 1/10

S1=  {0,03} over {1-0,1} =  {0,3} over {9}

S2=0,2+  {3} over {90} =  {21} over {90}

Semana:4

Vídeo:13

Docente: José Luiz Pastore Mello

Tema: Médias para todos os fins (I)

https://www.youtube.com/watch?v=vSLyQrXlpsE

O estudo das médias é muito diversificado, pois existem vários tipos de definições, mas é preciso saber que entre as médias existem três principais sendo elas: aritmética, geométrica e harmônica. A média aritmética foi definida como o excesso do primeiro número sendo ele igual para o segundo número e para o terceiro número, já a média geométrica ocorre quando a proporção de um número oferece seguimento para o segundo número que se dirige para o terceiro número, sendo ele igual a proporção do primeiro número para o segundo, e a  média harmônica ocorre quando a quantidade de excedência do primeiro número excede o segundo número, sendo isso em relação ao terceiro número. Contudo, essas formas são as mais utilizadas, mas existem várias maneiras de serem definidas. A ordenação das médias deve ser feita através da ação que estabelece as relações, pois a igualdade entre as três médias só ocorre quando o x for igual ao y. 

As imagens são representadas nessa situação por meio de um gráfico que contêm todos os dados necessários para formulação da estrutura.
Fonte: www.scielo.br

Vídeo:14

Docente: José Luiz Pastore Mello

Tema: Médias para todos os fins (II)

https://www.youtube.com/watch?v=oLXLw4t6eiY

 A média quadrática define a raiz quadrada da média aritmética entre os números e isso faz com que a fórmula seja modificada. Sua comparação entre as três médias mais comuns define que é a maior média entre todas. Para podermos compreender essa média é necessário utilizarmos as circunferências, pois através dela podemos fazer os cálculos das médias, onde o diâmetro é representado por traços que perpendiculam os pontos. A relação entre as médias podem ser verificadas através do comprimento entre as medidas de x e y. Sempre a menor das quatro médias (harmônica) e a maior (quadrática) terão a variação entre o x e o y com geração de circunferência igual. 

Entre as representações das médias é preciso a presença de valores que estabeleçam as relações a serem analisadas.

Fonte: www.itau.com.br
           www.scielo.br

Vídeo:15

Docente: Walter Spinelli

Tema: Probabilidades e Estatística: noções iniciais, contagem direta e indireta, curva normal (I)

https://www.youtube.com/watch?v=2oGiQ3VySzU

O conhecimento da estatística é muito rico. Nós a utilizamos em todos os momentos do cotidiano humano, por esse motivo precisamos estar envolvidos entre os tópicos referentes a esse conteúdo. Sua preocupação é sobre as questões variáveis que possuem classificações com características únicas sendo elas: variáveis qualitativas (qualidade) e quantitativas (discretas- associadas ao processo de contagem, contínuas- associadas ao processo de medição). Por meio de tabelas podemos estabelecer todos os elementos utilizados e assim conseguimos distribuí-los de maneira adequada, pois quando representamos um gráfico precisamos ter em mente que as variações precisam estar referentes ao conteúdo estudado, onde quando falamos em variável qualitativa é preciso seguir um conceito demonstrado em forma de barras ou em forma de pizza, já em relação as variáveis quantitativas, elas são contínuas, onde e necessário saber o índice de estatura maior e menor para podermos especificar a relação com maior exatidão que refere-se a amplitude entre o maior e o menor número.

A estatística e a probabilidade confronta a relação dos cálculos permitindo a análise das representações.

Fonte:www.williamtoda.com
           www.tecciencia.ufba.br

Vídeo:16

Docente: Walter Spinelli

Tema: Probabilidades e Estatística: noções iniciais, contagem direta e indireta, curva normal (II)

https://www.youtube.com/watch?v=GK6jMAWY3jo

As medidas importantes entre as estatísticas podem ser estabelecidas por meio das amostragens mais comuns sendo elas: casual simples (sorteada aleatoriamente), sistemática (estabelece padrão), acidental (precisa de pessoas certas) e estratificada (estabelece longa faixa de definição). Tendo esse conceito é possível fazer a escolha apropriada para determinada amostra com atuação da média e do desvio padrão necessário. Quando estamos em variáveis contínuas às curvas estabelecidas são as normas, mas ela sofre a tradução de uma expressão matemática que permite a construção de um gráfico. O estreitamento das curvas estabelecidas define os padrões com curvas mais fechadas, pois os dados estão representados de forma menos dispersa, já as curvas mais distantes definem valores espalhados. Com isso, o desvio padrão é importante para estabelecer a probabilidade a ser definida. 

Esses dois recursos são muito apropriados para sanar dúvidas de conceitos variados.
Fonte: www.etecribeiraopires.com.br 
Exercícios / aulas 13 e 14 

Os exercícios da aula 13 foram formulados para que pratique aquilo que aprendeu na vídeo aula. Para avaliação da aula 13, escolha pelo menos UM (1) exercício para resolver. A resposta deve ser enviada pelo Portfólio da disciplina.

Exercícios da aula 13

Conforme a solicitação de resolução dos exercícios, optei em solucionar o nº 04.

  Três torneiras ligadas sozinhas enchem um tanque em 3 h, 4 h e 6 h, respectivamente. Ligando as três torneiras simultaneamente, quanto tempo elas levarão para encher o tanque?

Exercícios da aula 14

Conforme a solicitação de resolução dos exercícios, optei em solucionar o nº 01.

Se x e y são números reais positivos tais que x=y, o que ocorre com a

ordenação entre as médias aritmética, geométrica, harmônica e quadrática?

Exercícios / aulas 15 e 16

 Exercícios da aula 15

Conforme a solicitação de resolução dos exercícios, optei em solucionar o nº 01.

  Determine a média, a moda e a mediana da seguinte distribuição

de frequências:

intervalo            freqüência             resultado

[2,8[                         4                              4

[8,14[                       6                             10

[14,20[                     8                             18

[20,26]                     6                             24

Por exemplo, em [2,8[ temos um intervalo “fechado” em 2 e “aberto” em 8, ou seja, 2 é um valor que pertence ao intervalo e 8 não pertence.

Média: 

Moda = 17
Mediana = 15,5.

Exercícios da aula 16

 Conforme a solicitação de resolução dos exercícios, optei em solucionar o nº 02.

No caso das alturas das pessoas cuja média é 1,60 m e o desvio 0,20

m, qual é o percentual de pessoas da população com altura entre 1,60 m

e 1,70 m?

Semana:5

Vídeo:17

Docente: Nilson José Machado

Tema: Expoentes e Logaritmos (I)

https://www.youtube.com/watch?v=W_Rh8_HJsao

 Logaritmos surgiram através da percepção dos números pois a análise de um cálculo é mais simplificada permitindo a compreensão através da utilização do recurso por ele oferecido que simplifica contas extensas e facilita o entendimento. Afinal, existem muitas expressões numéricas que devido a quantidade de elementos necessita de um recurso rápido para resolução dos problemas. Com tudo, criou-se a tabela logaritma sendo ela desenvolvida no século XVII para representar os cálculos de forma mais simplificada. Atualmente podemos ter acesso a este recurso facilmente.

Fonte: www.portalsaofrancisco.com.br

          www.slideplayer.com.br

Vídeo:18

Docente: Nilson José Machado

Tema: Expoentes e Logaritmos (II)

https://www.youtube.com/watch?v=Bm0DJ2rqpcg

A medida da intensidade sonora necessita da utilização dos logaritmos. Quando um som é produzido, sua intensidade sonora pode variar e com isso podemos visualizar a variação que torna o expoente o solucionador do problema. A escala de proporção permite o surgimento de outros recursos direcionados a expressar um número de outra maneira. Os logaritmos possuem muitas propriedades decorrentes de suas potências. As propriedades das potências nos cálculos matemáticos são levadas para as propriedades decorrentes dos logaritmos. Quando temos uma tabela em base A basta pegar todos os elementos e dividi-lo na base B. Portanto, as tabelas velhas podem ser aproveitadas como modelo de base para construção de uma nova tabela.

Fonte: www.portalsaofrancisco.com.br

          www.slideplayer.com.br

Vídeo:19

Docente: Walter Spinelli

Tema: Periodicidade na natureza: Trigonometria (I)

https://www.youtube.com/watch?v=5ZssTdQL__E

 Periodicidade esta ligada aos fenômenos que são ajustados de acordo com as nossas necessidades, afinal tudo que vivenciamos em nosso dia a dia se refere a ela. Um exemplo muito comum é em relação ao ajuste de horário e até mesmo o nascer do sol que em certas estações do ano sofre alteração. As variáveis de sombra permitem a elaboração de uma escala comparativa das relações de verão. Os gráficos são recursos úteis por representar a necessidade a ser analisada. A periodicidade está presente em vários momentos da vida humana, pois toda a comunicação vivenciada diariamente se baseia nas ondas magnéticas que é expressada como um meio de comunicação.

Fonte: www.grupoescolar.com

           www.matematiques.com.br

Vídeo:20

Docente: Walter Spinelli

Tema: Periodicidade na natureza: Trigonometria (II)

https://www.youtube.com/watch?v=F0N0wIsc_9s

Os pontos que percorrer a circunferência refere-se à intensidade e a proporção e na medida em que as equações recebem parâmetros acabam sofrendo mudanças. As alterações gráficas devem ser realizadas a partir dos parâmetros que fazem com que o gráfico seja distorcido para cima ou para baixo. As características das ondas possuem a velocidade, a freqüência e o período que se adaptam as proporções variáveis associadas. Quando as constantes se aumentam o comprimento acaba se diminuindo fazendo com que sua freqüência seja aumentada.  As constantes têm relação com as ondas e em nossa realidade pode ser aplicada na natureza. Sabe-se que o eixo da terra determina o índice de claridade e o cálculo elaborado a partir da equação trigonométrica facilita a elaboração da equação e permite a compreensão do problema.

Fonte: www.slideplayer.com.br
Exercícios da semana 5 - vídeoaulas 17 e 18

A) Para avaliação das aulas 17 e 18 da Semana 5 da disciplina, escreva um resumo pessoal, de 10 a 20 linhas, sobre o significado do tema tratado, registrando em que as aulas contribuíram para revelar o papel da Matemática na compreensão da realidade. Publique sua resposta no Portfólio da disciplina.

B) Os exercícios das aulas 17 e 18, foram formuladas a partir de pequenos textos (Texto A, Texto B, Texto C etc.). Para avaliação das aulas 17 e 18, escolha pelo menos UM (1) Texto (A, B, C etc.) e resolva os exercícios relacionados ao texto. As respostas devem ser enviadas pelo Portfólio da disciplina. Para melhorar a sua aprendizagem resolva, explore e aprofunde, até onde for possível, os outros textos e seus exercícios.

Expoente e Logaritmo

Por meio dessas aulas compreendi a importância da utilização do expoente e do logaritmo, pois as fórmulas expressadas por esses recursos facilitam a compreensão de exercícios além de permitir o desenvolvimento de alguns problemas. Quando estamos diante de cálculos muito extensos, é por meio desses recursos que conseguimos resolvê-los com mais facilidade. Portanto, ao utilizar as regras como, por exemplo: fazer a transformação de uma operação de um número x com base y onde aplicamos a base para obter o resultado além de facilitar permite a compreensão.

“O logaritmo de um número b em uma base a é o expoente x que se deve aplicar à base a para se ter o número b. A idéia fundamental dos LOGARITMOS é transformar as operações de multiplicação em soma (e de divisão em subtração). Na verdade, o logaritmo é uma nova denominação para um expoente”.

A matemática faz parte da vida humana, estando presente em todas as situações do nosso dia a dia, por isso é preciso haver uma compreensão de suas regras para podermos utilizá-la de forma correta e segura no desenvolvimento dos problemas.

Como foi visto em aula, os logaritmos são utilizados para tornar números muito grandes ou muito pequenos mais facilmente perceptíveis, associando-os a números menores. Em vez de 107 ou 10-7 , penso nos expoentes 7 ou no -7. O logaritmo de um número N é apenas o expoente da potência de 10 que expressa o valor de N: log N = n quer dizer que 10n = N. Na verdade, qualquer outra base poderia ser utilizada, mas a conveniência da base 10 nos cálculos cotidianos torna o começo do estudo por essa base mais natural. Quando a base for diferente de 10, isso precisa ser destacado. Assim, se N = ax  então x = logaritmo de N na base a = logaN. De modo geral, os números que correspondem a potências inteiras da base têm logaritmos inteiros; os outros, têm logaritmos fracionários, sendo a grande maioria números irracionais. Desde o século XVII são construídas tabelas que fornecem os valores aproximados de tais expoentes.

Sendo dados os valores aproximados log 2 = 0,30 e log 3 = 0,47, preencha a tabela abaixo:

N	N = 10n	n    (log N)
1	1 = 100	0
2	2 = 100,30	0,3
3	3 = 100,47	0,47
4	4 = 102×0,30	0,60
5	5 = 101-0,30	0,70
6	6 = 100,30+0,47	0,77
8	8 = 103×0,30	0,90
9	9 = 102×0,47	0,94
10	10 = 101	1
12	12 = 100,47+0,60	1,07
15	15 = 100,47+0,70	1,17
18	18 = 100,30+0,94	1,24
20	20 = 101+0,30	1,30
27	27 = 100,47+0,94	1,41
30	30 = 100,47+1	1,47
32	32 = 105×0,30	1,50
36	36 = 100,60+0,94	1,54
40	40 = 100,60+1,00	1,60
60	60 = 100,77+1	1,77
100	100 = 102	2
300	300 = 100,47+2	2,47
400	400 = 100,60+2	2,60
1000	1000 = 103	3
3000	3000 = 100,47+3	3,47
9000	9000 = 100,94+3	3,94
10000	10000 = 104	4
50000	50000 = 100,70+4	4,70
100000	100000 = 105	5

Exercícios da semana 5 - vídeo aulas 19 e 20

Nesta semana, a sua avaliação para as Aulas 19 e 20 será composta por duas entregas no Portfólio de Matemática que estão descritas a seguir:

A) Os exercícios da aula 19 foram formulados para que pratique aquilo que aprendeu na vídeoaula. Para avaliação da aula 19,escolha pelo menos UM (1) exercício para resolver. A resposta deve compor o Portfólio da disciplina. Para melhorar a sua aprendizagem resolva, explore e aprofunde, até onde for possível, os outros exercícios da aula 19.

B) Os exercícios da aula 20, foram formulados para que pratique aquilo que aprendeu na vídeoaula. Para avaliação da aula 20, escolha pelo menos UM (1) exercício para resolver. A resposta deve compor o Portfólio da disciplina. Para melhorar a sua aprendizagem resolva, explore e aprofunde, até onde for possível, os outros exercícios da aula 20. 

Qual é o período e a imagem da função f(x)=3+4sen(x3)? 

 Faça um esboço do gráfico da função.

Numa função do tipo f(x)=a+b⋅sen(r⋅x+q).

O período T é dado pela fórmula: A imagem da função: Im(f)={y∈R|−1≤y≤7}

 Desenhe dois períodos do gráfico da função f(x) = 3sen 4x.

Semana: 6
Vídeo: 21

Docente: Nilson José Machado

Tema: Ideias Fundamentais do Cálculo / Funções do 2º grau (I)

https://www.youtube.com/watch?v=_nnOMqQoynA

 Existem algumas idéias que permitem o pensamento da matemática sendo em principal, quando nos referimos aos cálculos que fazem o reconhecimento de idéias fundamentais. Faz parte da matemática o saber da proporcionalidade, pois assim podemos olhar para a questão de forma, a saber, solucioná-la. A aproximação de algo variável e constante deve ser raciocinada a uma idéia de algo que seja integral. Se pensarmos que as variações das funções são expressadas através de várias maneiras, podemos compreender que as regras para a elaboração de uma questão nos permite direcionar o pensamento para a forma correta de compreensão. Em qualquer nível de observação das relações variáveis calculáveis podemos definir que as funções de proporções podem ser simples ou complexas. Se todas as grandezas fossem diretamente proporcional seria muito fácil compreender e desenvolver as relações.

Vídeo: 22

Docente: Nilson José Machado

Tema: Ideias Fundamentais do Cálculo / Funções do 2º grau (II)

https://www.youtube.com/watch?v=ljfdwKUCOU0

Uma função constante não sofre alteração, já uma função variável permite modificações e quando a unimos é possível compô-las raciocinando a constante delas e isso forma a sucessão de degraus que aproximam as variáveis e as constantes. Quando consideramos algo variável e constante em pequenos intervalos conseguimos integrar uma função formando outras áreas. As variações permitem as aproximações. A função do segundo grau permite que a taxa de variação seja variável, mas a taxa da taxa se torna constante. Se utilizarmos todos os recursos para realização dos cálculos matemáticos poderemos desenvolver um ótimo resultado em relação a estrutura formada pela matemática.

Vídeo: 23

Docente: José Luiz Pastore Mello

Tema: Geometrias não euclidianas - uma introdução (I)

https://www.youtube.com/watch?v=rMUIzmZsYuM

As variações da geometria permite-nos compreender que surgiram por matemáticos especializados na dinâmica dos cálculos. Entre o período do renascimento ocorreu a descoberta do famoso pai da geometria ( Euclides) que organizou a geometria através de verdades com presença de evidências com a construção de pensamentos sobre os postulados ( 1º cria a regra através de dois pontos onde nele passa duas retas; 2º define que uma linha reta pode ser expressa de várias maneiras; 3º expressa que podemos traçar um círculo de várias formas; 4º  informa que todos os ângulos retos são iguais e o 5º conclui que entre o plano posterior existe uma única reta com um ponto paralelo). Por meio desses cinco elementos foi construída a geometria. Diante desse conceito podemos perceber que as variações geométricas nos permitem desenvolver técnicas associativas e práticas para o desenvolvimento dos exercícios.

Vídeo: 24

Docente: José Luiz Pastore Mello

Tema: Geometrias não euclidianas - uma introdução (II)

https://www.youtube.com/watch?v=XtHQfW01ERY

A geometria não euclidiana surge com Euclides que elaborou a estrutura do pensamento geométrico propondo os cinco postulados, mas modernamente ocorreu a revisão da geometria chegando a conclusão por Hilbert que fez a releitura dos axiomas de Euclides dizendo qual seriam os postulados realmente necessários para a estrutura geométrica.  Diante dos axiomas, Hilbert define que os pontos estabelecidos permitem variações de fórmulas que podem ser desenvolvidas e que os dois pontos mais utilizados geram a raiz quadrada com resolução de todas as distâncias. A nova geometria é chamada de taxista, pois, com a divisão das estruturas fica mais fácil compreender as distâncias dos pontos estabelecidos. A geometria do taxista produz resultados inusitados, pois sua circunferência fica eqüidistante ao ponto expressado. Portanto, os conjuntos dos pontos infinitos formam um quadrado e com isso essa geometria gera um quadrado com resultados diferentes.

Este conteúdo esta em fase de construção.

Exercícios da semana 6 - vídeoaulas 21 e 22

Nesta semana, a sua avaliação para as Aulas 21 e 22 será composta por duas entregas no Portfólio de Matemática que estão descritas a seguir:

Os exercícios das aulas 21 e 22, foram formuladas a partir de pequenos textos (Texto A, Texto B, Texto C etc.). Para avaliação das aulas 21 e 22, escolha pelo menos DOIS (2) Textos (A, B, C etc.) e resolva os exercícios relacionados ao texto. As respostas devem ser enviadas pelo Portfólio da disciplina. Para melhorar a sua aprendizagem resolva, explore e aprofunde, até onde for possível, os outros textos e seus exercícios. Lembre-se - Nesta semana você também deverá postar a resolução de alguns exercícios referentes as vídeo aulas 23 e 24 que estão disponíveis na Organização Didática da semana 6 e no Ambiente Virtual de  aprendizagem (AVA) do curso.

Exercícios da semana 6 - vídeo aulas 23 e 24

RECOMENDAÇÕES GERAIS SOBRE A AVALIAÇÃO (PORTFÓLIO)

Caro aluno,

Nesta semana, a sua avaliação para as Aulas 23 e 24 será composta por duas entregas no Portfólio de Matemática que estão descritas a seguir:

A) Os exercícios da aula 23 foram formulados para que pratique aquilo que aprendeu na vídeoaula. Para avaliação da aula 23, escolha pelo menos UM (1) exercício para resolver. A resposta deve compor o Portfólio da disciplina. Para melhorar a sua aprendizagem resolva, explore e aprofunde, até onde for possível, os outros exercícios da aula 23.

B) Os exercícios da aula 24, foram formulados para que pratique aquilo que aprendeu na vídeoaula. Para avaliação da aula 24, escolha pelo menos UM (1) exercício para resolver. A resposta deve compor o Portfólio da disciplina. Para melhorar a sua aprendizagem resolva, explore e aprofunde, até onde for possível, os outros exercícios da aula 24.

Matemática – vídeo aula 23

Geometrias não euclidianas

Prof. José Luiz Pastore Mello

Exercícios

1.       Considere uma esfera de isopor de 20 cm de diâmetro, que está sendo usada para representar a Terra, cujo raio é de aproximadamente 6371 km. Determine a escala de comprimentos utilizada nessa representação.

Para transformar seu diâmetro em raio você deve dividir por 2 então 20 / 2 = 10
depois a formula fica assim E= d/DE =   6371km / 10 você precisa transformar os cm em km 10 cm / 100 000= 0,0001 6371/ 0,0001 = 63710000 então aproximadamente 1:64 000 000 ou pode por o valor exato 1 : 63 710 000

Texto C

A ideia de integral é fortemente associada ao conceito de área: calcular a integral de uma
função pode ser interpretado como calcular uma área sob o gráfico de uma função.
Na página http://calculusapplets.com/riemann.html é presente uma aplicação para calcular a
área de várias curvas (hipérbole, parábola, semicircunferência, etc. ). O método consiste em
aproximar trechos da função com trechos constantes, obtendo assim vários retângulos, dos
quais o software pode facilmente calcular a área. Cada aproximação é feita por falta
(retângulos “blue”) e por excesso (retângulos “pink”).
1. Considere a hipérbole representada pela função y = 1/x

TEXTO D
Como foi visto na videoaula, a ideia de integral pode ser útil também para calcular o valor
médio de uma função. A ideia é a seguinte: entre dois valores de
x, a e b por exemplo, o gráfico de uma função f(x) e o eixo dos x
delimitam certa área; o valor médio da função é o que
corresponde ao ponto c, entre a e b, tal que o retângulo de base
b-a e de altura f(c) tem área igual à sob o gráfico de f(x) no mesmo
intervalo.
1. Utilizando a aplicação presente no site http://calculusapplets.com/aveval.html, calcule
o valor médio da função f(x) entre o intervalo [0,3]. Copie e cole o gráfico obtidos
pelo aplicativo.
Observação: o software utiliza um número finito de retângulos para aproximar a área,
então tanto a superfície quanto o valor médio serão aproximados.

Semana: 7

Vídeo: 25

Docente: Walter Spinelli

Tema: Matemática e Física: relação simbiótica (I)

https://www.youtube.com/watch?v=Htnv9GNO3KE

 A interdisciplinaridade é evidente na matemática, sendo através das idéias fundamentais matemáticas que permitem a exploração das evidências. As proporcionalidades estão diretamente relacionadas à física. Diante dos conceitos existentes é possível desenvolver as habilidades, mas para elaborar-mos precisamos estar atentos ao conjunto da mecânica que se referem aos efeitos de deslocamento, tudo isso correspondente a taxa de variação dos eixos verticais e horizontais. Os efeitos de movimento uniforme e acelerado oferecem a proporcionalidade e a funcionalidade.

Vídeo: 26

Docentes: Walter Spinelli

Tema: Matemática e Física: relação simbiótica (II)

https://www.youtube.com/watch?v=e30Bf0qmfjs

A matemática estrutura a física, pois ocorre uma relação simbiótica. Relações de proporcionalidade possuem variações sendo expressas em vários conteúdos da física. O calor pode ser explorado através de escalas termométricas. Na transformação das escalas é possível desenvolver a relação entre os graus, mas, a proporcionalidade depende da forma de expressão do exercício. As representações das equações podem ser relacionadas de acordo com as diversidades representadas. O aquecimento oferece outra forma de diversidade da representação isso por meio de uma tabela que consegue exemplificar todos os conceitos necessários e de forma clara. A variação da temperatura é exemplificada com gráficos iniciados no ponto zero. A exploração da curva de crescimento possibilita a compreensão além de permitir as variedades de explorações sobre as etapas de uma escala.

Vídeo: 27

Docentes: Carlos Eduardo S.C. Granja

Tema:  Matemática e Música (I)

https://www.youtube.com/watch?v=ETPzsN-vgE8

A relação da matemática com a música surgiu com a interação de quatro itens que possuíam uma articulação interna com junções. A relação geométrica e a relação da astronomia também interferiram nessa relação. O primeiro filósofo que trabalhou com essa relação foi o Pitágoras que construiu a primeira escala musical sendo fundamental para a afinação dos instrumentos. A primeira relação entre números e sons ocorreu após a interação entre uma oficina de ferreiros. Pitágoras ao ouvir sons agradáveis (sons que geram harmonia entre si), por outro lado as formas diferenciadas (definem sons ruidosos e inconvenientes). Ao pesar barras, descobriu a relação entre os pesos e para isso utilizou o monocórdio que permitiu a relação de sons com diferentes relações. As relações entre os sons e as frações podem ser distinguidas quando ocorre a harmonização dos sons, sendo eles equivalentes. Os princípios de construção definem que toda nota é equivalente, mas o ciclo é representado por 2/3 que define o limite de espectro entre as metades e os inteiros. As escalas pitagóricas exigem regras que devem ser elaboradas para permitir a representação dos produtos a serem estabelecidos.

Vídeo: 28

Docentes: Carlos Eduardo S.C. Granja

Tema:   Matemática e Música (II)

https://www.youtube.com/watch?v=GFZngfZU6Yk

Os aspectos físicos da música e do som são diferenciados, onde Pitágoras construiu a definição de que a matem tica regia a música, mas não ocorre o substrato da categoria teórica sobre esse sentido. As conseqüências dos sons definem as diversificações. Os sons são propagados no ar na forma de ondas. A representação do som como onda permite a relação entre a variação de pressão e tempo percorrido. A compressão e a rarefação liberação a interferência das relações e o número de vibrações podem ser exemplificados de várias formas. Existe relação inversa quando referente ao comprimento da corda e a relação de sua fração com possibilidade de freqüência. O processo de desenvolvimento da esfera pitagórica foi modificado por possuir defeitos, afinal, ao se criar escalas esperam-se a criação de notas equivalentes. O ciclo pitagórico não se fecha e forma um ciclo espiral. Portanto, as quintas e as oitavas não se combinam.

Exercícios da semana 7- vídeoaulas 25 e 26

 Caro aluno,

Nesta semana, a sua avaliação para as Aulas 25 e 26 será composta por duas entregas no Portfólio de Matemática que estão descritas a seguir:

A) Os exercícios da aula 25 foram formulados para que pratique aquilo que aprendeu na vídeo aula. Para avaliação da aula 25, escolha pelo menos UM (1) exercício  para resolver. A resposta deve ser  enviada pelo Portfólio da disciplina.  Para melhorar a sua aprendizagem resolva, explore e aprofunde, até onde for possível, os outros exercícios da aula.

B) Os exercícios da aula 26, foram formulados para que pratique aquilo que aprendeu na vídeo aula. Para avaliação da aula 26, escolha pelo menos UM (1) exercício  para resolver. A resposta deve ser  enviada pelo Portfólio da disciplina.  Para melhorar a sua aprendizagem resolva, explore e aprofunde, até onde for possível, os outros exercícios da aula.

                        

      Exercícios da semana 7 - vídeoaulas 27 e 28

  RECOMENDAÇÕES GERAIS SOBRE A AVALIAÇÃO (PORTFÓLIO)

Caro aluno,

Nesta semana, a sua avaliação para as Aulas 27 e 28 será composta por 

duas entregas no Portfólio de Matemática que estão descritas a seguir:

A) Os exercícios da aula 27 foram formulados para que pratique aquilo que aprendeu na vídeo aula. Para avaliação da aula 27, escolha pelo menos UM (1) exercício para resolver. A resposta deve compor o Portfólio da disciplina. Para melhorar a sua aprendizagem resolva, explore e aprofunde, até onde for possível, os outros exercícios da aula.

B) Os exercícios da aula 28, foram formulados para que pratique aquilo que aprendeu na vídeo aula. Para avaliação da aula 28, escolha pelo menos UM (1) exercício para resolver. A resposta deve compor o Portfólio da disciplina. Para melhorar a sua aprendizagem resolva, explore e aprofunde, até onde for possível, os outros exercícios da aula.